Cardanovy hádanky a hlavolamy

Hranice mezi rekreační a „vážnou“ matematikou není vždy ostrá a zřetelná. Nemusí být zřejmé, kdy jde ještě jen o cvičení důvtipu a kdy řešení problému posouvá hranice poznání či přináší nějaký jiný užitek. Některé hlavolamy, hádanky a matematické prostocviky jsou známy již od starověku, i když jejich původní účel je třeba již zapomenut. Obliba matematických úloh chápaných jako cvičení důvtipu vzrostla v době renesance. Za první knihu věnovanou speciálně rekreační matematice je považováno dílo C. Bacheta Problèmes plaisants & délectables (1612). Bachet do své sbírky zařadil vedle vlastních úloh také problémy známé z prací jiných matematiků, mj. L. Pacioliho, Tartaglii a také G. Cardana. Cardano se ve svých knihách pojímaných občas jako celé encyklopedie lidského vědění věnoval i hádankám a hlavolamům, z nichž je zde vybráno několik příkladů.

Magické čtverce

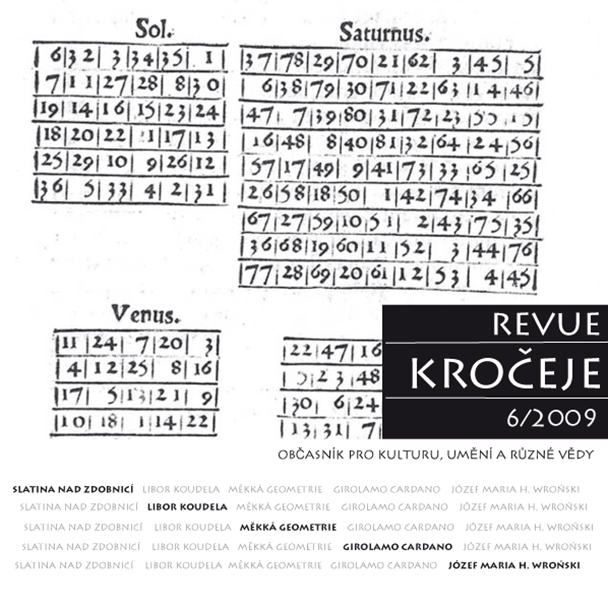
Magické čtverce jsou soubory čísel uspořádaných do čtverce, přičemž jejich součty v řádcích, sloupcích i diagonálách dávají stejný výsledek. Čisla v magickém čtverci jsou většinou po sobě jdoucí přirozená čísla počínající jedničkou. Jedná se o vcelku běžnou součást knih o rekreační matematice, zároveň však jde o jeden z těch problémů, které našly cestu i do „vážné“ matematiky (na začátku 20. století použil O. Veblen ke studiu magických čtverců metody teorie matic). Historie magických čtverců sahá až do starověké Číny. První doklady o jejich užití jako talismanů a o jejich přiřazení planetám a jejich géniům se objevují v pozdním středověku a na počátku novověku; nelze však vyloučit, že v magii hrály svou roli mnohem dříve. Nejznámějším spisem tohoto druhu je patrně dílo De occulta philosophia (1531) H. C. Agrippy z Nettesheimu, na nějž se odvolává i většina těch, kdo se v pozdější době zabývali způsobem využití magických čtverců v ceremoniální magii. Saturnu odpovídá čtverec 3x3, Jupiteru 4x4, Marsu 5x5, Slunci 6x6, Venuší 7x7, Merkuru 8x8 a Luně 9x9.

Girolamo Cardano se magickým čtvercům věnoval v knize Practica arithmeticae (1539), své první knize o matematice, která obsahovala především elementární poznatky z aritmetiky a algebry, ale zasahovala i do jiných oblastí, např. astrologie. Cardano uvádí tytéž čtverce jako Agrippa (v první polovině 16. století nebylo spektrum známých čtverců příliš široké); zajímavé ale je, že Cardano uvádí obrácené přiřazení než Agrippa nebo ještě dříve Cardanův krajan Pacioli.

Magické čtverce v Cardanově spisu Practica arithmeticae, 1539.

Cardanovo uspořádání magických čtverců (M. Folkerts je označuje jako Systém II) odpovídá starověkému uspořádání sedmi planet a sedmi nebeských sfér: Luna, Merkur, Venuše, Slunce, Mars, Jupiter, Saturn. Toto upořádání odráží průměrnou rychlost pohybu nebeských těles na obloze; Měsíc je nejrychlejší a bude tedy nejblíže Zemi, Saturn je nejpomalejší a jeho sféra bude od Země nejvzdálenější. Známý Cardanův sen o putování jeho duše nebeskými sférami odpovídal rovněž tomuto uspořádání. Mnohem rozšířenější obrácené pořadí (Systém I) může mít původ v hebrejské tradici, na niž se např. Agrippa často odvolává.

Josefův problém

Úloha XXIII Bachetovy sbírky je zadána takto: 15 křesťanů a 15 Turků se plaví po moři na jedné lodi, když je zastihne strašná bouře. Kapitán rozhodne, že polovina pasažérů musí být obětována, aby se zbývající část zachránila. Cestující utvoří kruh a začnou se odpočítávat s tím, že každý devátý bude obětován. Úkolem je najít takové rozestavení, aby prvních 15 vyřazených byli pouze Turci.

Jedná se o úlohu příbuznou s tzv. Josefovým problémem, o němž se Bachet zmiňuje v předmluvě své knihy. Flavius Josephus vypráví ve Válce židovské, jak spolu se čtyřiceti židovskými spolubojovníky našel úkryt v jakési jeskyni, když Římané dobyli Iótapatu. Zatímco Josef byl ochoten vzdát se Římanům, jeho muži chtěli dát přednost smrti před zajetím a byli rozhodnuti i Josefa raději zabít, než aby mu dovolili podrobit se.  Josef v důvěře v ochranu boží navrhl, aby nikdo nepadl vlastní rukou, ale aby se losovalo a vylosovaný padl vždy rukou toho, kdo bude vylosován po něm. Ostatní na to přistoupili a skutečně to nakonec byl Josef, kdo ještě s jedním zůstal poslední a tak unikl smrti.

V této verzi příběhu rozhoduje náhoda či boží prozřetelnost. Josefův problém, s nímž se občas setkávájí i dnešní studenti na kursech diskrétní matematiky, je zadán takto: Celkem n lidí utvoří kruh a jeden se vybere jako první. Od něj se odpočítává a každý k-tý účastník je vyřazen. Úkolem je najít takové místo v kruhu, na kterém se vydrží nejdéle.

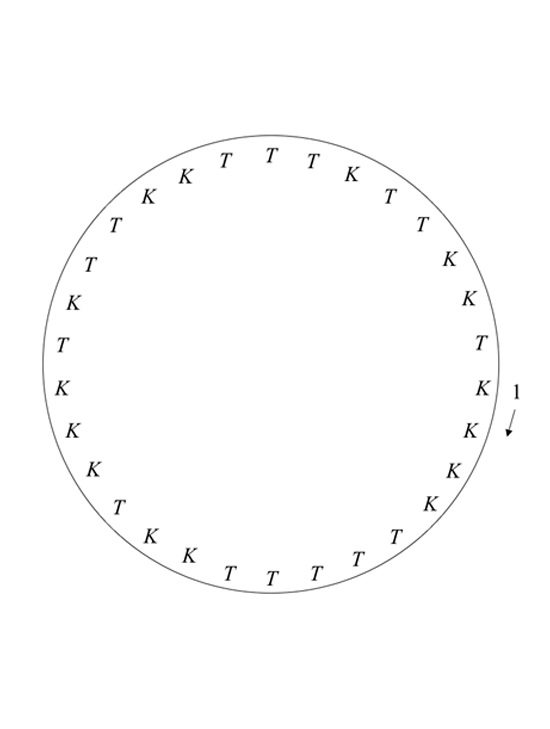Pokud by Turci přistoupili na toto rozestavení, byli by všichni vydáni napospas vlnám.

Úloha s Turky a křesťany se objevuje v různých historických údobích, přičemž charakteristiky obou skupin se liší v závislosti na prostředí. Cardano tuto úlohu popisuje v Practica arithmeticae, pouze místo křesťanů a Turků volí neutrální černé a bílé kameny. I když Cardano nebyl prvním, kdo takovou úlohu popsal, byl  zřejmě prvním, kdo ji spojil s Josefem (nazývá ji ludus Ioseph, tedy Josefova hra).

Cardanovy kruhy

Patrně nejznámějším hlavolamem spojovaným s Cardanem jsou tzv. čínské nebo též Cardanovy kruhy. Na vodorovném rameni jsou navléknuty kroužky opatřené rovnými držátky, jejichž konce jsou spojeny dohromady. Cílem je oddělit obě součásti od sebe. Pořadí kroužků nelze měnit a daný kroužek lze sejmout z ramene pouze tehdy, když sousední kroužek směrem k volnému konci je navlečen, ale všechny další jsou dole. První kroužek (příp. první dva) lze volně sejmout.

Původ a účel tohoto zařízení, jemuž Francouzi říkají baguenaudier, není úplně jasný; mohlo snad sloužit jako zámek. Obě součásti nejsou topologicky propojené, ale jejich oddělení vyžaduje velký počet úkonů. Cardano popisuje toto zařízení v knize De subtilitate (1550). Podrobný popis hlavolamu lze najít např. v knize W. W. Rouse-Balla Mathematical Recreations and Essays nebo v díle Récréations mathématiques E. Lucase, který podává rovněž etymologický rozbor francouzského názvu. Lucas s odvoláním na knihu Théorie du Baguenodier L. Grose uvádí elegantní matematické řešení problému pomocí binárního kódování.

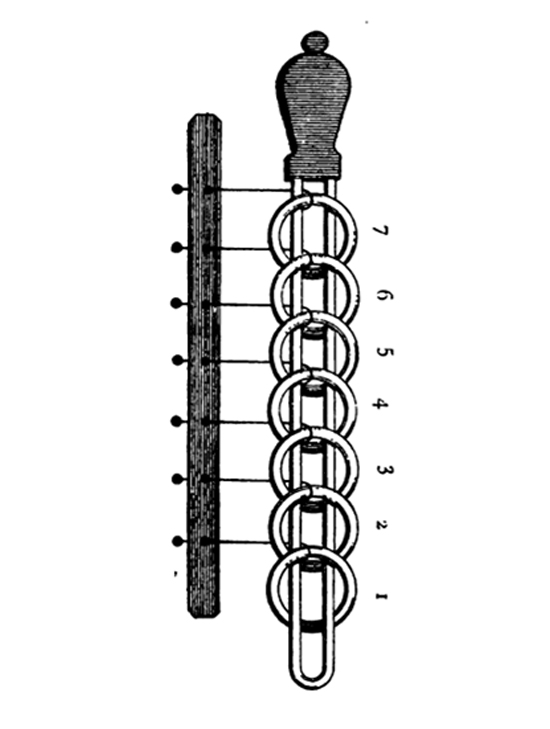Vyobrazení Cardanových kruhů v knize E. Lucase Récréations mathématiques (Paris 1882)